Thursday, December 20, 2012
Wednesday, December 19, 2012
HW for Friday
Revisit the Ripple applet and play with the "two sources" set-up. It may be helpful to look at the different color schemes.
http://falstad.com/ripple/
You are witnessing waves "interfering" with each other.
This can happen quite easily with light - passing light through small openings creates "diffraction" patterns.
Look into this phenomenon, checking out images online.
Also, see if you find out some information about this equation:
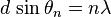
Detailed info here - you don't have to read the entire thing, but have a look if there is time:
http://en.wikipedia.org/wiki/Diffraction
Finally, if you're bored over break and want to read ahead, look into HOLOGRAPHY.
http://falstad.com/ripple/
You are witnessing waves "interfering" with each other.
This can happen quite easily with light - passing light through small openings creates "diffraction" patterns.
Look into this phenomenon, checking out images online.
Also, see if you find out some information about this equation:
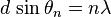
Detailed info here - you don't have to read the entire thing, but have a look if there is time:
http://en.wikipedia.org/wiki/Diffraction
Finally, if you're bored over break and want to read ahead, look into HOLOGRAPHY.
Thursday, December 13, 2012
Today / Thursday
This is the last day I expect to be out. I hope to return tomorrow (Friday) and will keep G and X block open for lab questions, etc.
TURN IN A DRAFT TODAY IF YOU WANT IT BACK FOR COMMENTS TOMORROW. There will be a box on the front desk in the classroom - turn them in there.
Formal lab is due next Wednesday.
Problems to try in class TODAY. Work on these and discuss. These are NOT to turn in, but you should be discussing them in your lab group.
The following equations will be needed:
Lens/mirror equation:
1/f = 1/do + 1/di
Magnification equation:
M = -di/do
1. You have a convex lens with focal length (f = 20 cm). Where do you find the image (di) if the object is located (do):
a. 100 cm away
b. 40 cm away
c. 30 cm away
d. 20 cm away
e. 10 cm away
Solve first, then check your answers below.
Look at cases b, d and e in particular. Is there anything strange about the answers these cases? Do you notice any similarities with your lab data?
Looking at e -- if you've done it correctly, you calculated a negative answer. What do you think a negative di means about the image?
Looking at d -- this one is hard to think about, but the answer is "undefined." What does this mean?
Answers:
a. 25 cm
b. 40 cm
c. 60 cm
d. undefined (or di = infinity); no image is seen, or the light rays emerge parallel (never converging, or rather, converging at infinity)
e. -20 cm
2. Now go back to problem 1 and calculate the magnifications in each of the cases.
Answers:
a. -0.25
b. -1
c. -2
d. no image
e. 2
Worth noting:
Magnification means how much the image is magnified (compared to the object).
Magnification has no units - it is a ratio that represents how many times the image is larger than the object.
A negative magnification means that the image is upside-down.
When the absolute value of the magnification is greater than 1, the image is larger than the object.
When the absolute value of the magnification is less than 1, the images is smaller than the object.
If the absolute value of the magnification equals 1, the image is the same size as the object.
If there is time in class, you may continue to work on the lab draft, but it must be turned in today (in the box on my front lab desk) for me to look at it tonight and return it tomorrow (to your mailbox).
Revisit the applet and play around. Note that you can change the optic from convex to concave, and from lens to mirror. Slide the arrow (object) from left to right and note how the image changes.
TURN IN A DRAFT TODAY IF YOU WANT IT BACK FOR COMMENTS TOMORROW. There will be a box on the front desk in the classroom - turn them in there.
Formal lab is due next Wednesday.
Problems to try in class TODAY. Work on these and discuss. These are NOT to turn in, but you should be discussing them in your lab group.
The following equations will be needed:
Lens/mirror equation:
1/f = 1/do + 1/di
Magnification equation:
M = -di/do
1. You have a convex lens with focal length (f = 20 cm). Where do you find the image (di) if the object is located (do):
a. 100 cm away
b. 40 cm away
c. 30 cm away
d. 20 cm away
e. 10 cm away
Solve first, then check your answers below.
Look at cases b, d and e in particular. Is there anything strange about the answers these cases? Do you notice any similarities with your lab data?
Looking at e -- if you've done it correctly, you calculated a negative answer. What do you think a negative di means about the image?
Looking at d -- this one is hard to think about, but the answer is "undefined." What does this mean?
Answers:
a. 25 cm
b. 40 cm
c. 60 cm
d. undefined (or di = infinity); no image is seen, or the light rays emerge parallel (never converging, or rather, converging at infinity)
e. -20 cm
2. Now go back to problem 1 and calculate the magnifications in each of the cases.
Answers:
a. -0.25
b. -1
c. -2
d. no image
e. 2
Worth noting:
Magnification means how much the image is magnified (compared to the object).
Magnification has no units - it is a ratio that represents how many times the image is larger than the object.
A negative magnification means that the image is upside-down.
When the absolute value of the magnification is greater than 1, the image is larger than the object.
When the absolute value of the magnification is less than 1, the images is smaller than the object.
If the absolute value of the magnification equals 1, the image is the same size as the object.
If there is time in class, you may continue to work on the lab draft, but it must be turned in today (in the box on my front lab desk) for me to look at it tonight and return it tomorrow (to your mailbox).
Revisit the applet and play around. Note that you can change the optic from convex to concave, and from lens to mirror. Slide the arrow (object) from left to right and note how the image changes.
For homework, continue to work on lab report - I will return your labs to your mailboxes on Friday. You can also look at these problems and the applet again.
Monday, December 10, 2012
About the lab
There is apparently panic brewing. The DRAFT of the lab is due on Thursday. You will have time tomorrow to work on it, though you should have done a good amount of it by now.
The FINAL copy of the lab will be due NEXT Wednesday (before winter break begins).
Got it?
In your lab, be sure to have all the important lab stuff:
purpose
hypothesis (this was hw from before the beginning of the lab)
data tables
sample calculations
questions that were posted last time
conclusion, etc.
I will be out tomorrow (Tuesday).
The FINAL copy of the lab will be due NEXT Wednesday (before winter break begins).
Got it?
In your lab, be sure to have all the important lab stuff:
purpose
hypothesis (this was hw from before the beginning of the lab)
data tables
sample calculations
questions that were posted last time
conclusion, etc.
I will be out tomorrow (Tuesday).
Friday, December 7, 2012
Lab questions
Questions for the lens/mirror lab:
1. 1, You’ve no
doubt seen that the size of the image changes.
Comment on how/where it changes.
Knowing the theoretical focal length, can you determine a rule (or an
approximate rule) – something like, the image goes from smaller to larger when
do is equal to the focal length (or something like that). Be specific.
2. 2. How does the aperture affect the image? That is, if you were to block the top part of
the lens or mirror, how would the image change?
How about if you cover the bottom part?
3. 3. You should calculate theoretical focal lengths
for every point where you have data (do and di). How do these experimental focal lengths
compare to the theoretical focal length? Do a percent difference calculation for each.
4. 4, In general, have you found your results for
lenses and mirrors to be similar?
Discuss.
5. 5. In this lab, where did you see virtual
images? How did you know they were virtual?
6. 6. How could one determine (experimentally) the focal
length of a convex mirror or concave lens?
7. 7. Mathematically, there are worthwhile cases to
consider – key points – where do = f, do = 2f, do is much, much greater than f. What is going on mathematically with each of
these cases?
8. 8. Don’t forget to give errors and a general
conclusion. In your conclusion, discuss
the extent to which your initial suspicions (hypothesis) were correct or
incorrect.
Play around with this applet and note what
happens. This may make things easier to
visualize, even though only 2 or 3 rays are depicted as coming from the object.
There is a useful expression, the
magnification equation:
Magnification = -di/do
In this equation, a negative magnification
indicates an upside down image. If the
absolute value of the magnification is greater than 1, the image is
larger. You may want to calculate
magnifications to see how well they match with what you find to be in the lab
data.
Wednesday, December 5, 2012
HW
Don't forget - brief quiz (Snell's law) on Friday. Invest a few minutes in reviewing/studying.
To prepare for last day of lab stuff:
Investigate the difference between real images and virtual images. Define each.
If you have time, calculate experimental focal lengths, using the thin lens equation:
1/f = 1/do + 1/di
(It's easiest if you use the x^-1 key on the calculator.)
Continue to examine lab data and look for trend(s).
To prepare for last day of lab stuff:
Investigate the difference between real images and virtual images. Define each.
If you have time, calculate experimental focal lengths, using the thin lens equation:
1/f = 1/do + 1/di
(It's easiest if you use the x^-1 key on the calculator.)
Continue to examine lab data and look for trend(s).
Monday, December 3, 2012
HW
1. Examine lab data; look for trends.
2. Look up: thin lens equation. Find out how what it means, how to use it, etc.
3. Look up concave and convex mirrors - know the difference.
Also - suggested viewing from Alexis (thanks!). You may find some useful videos here:
http://www.khanacademy.org/science/physics
2. Look up: thin lens equation. Find out how what it means, how to use it, etc.
3. Look up concave and convex mirrors - know the difference.
Also - suggested viewing from Alexis (thanks!). You may find some useful videos here:
http://www.khanacademy.org/science/physics
Thursday, November 29, 2012
homework for Monday
A few things to do for Monday:
1. Review the concept of critical angle and the related formula.
2. Calculate the critical angle of diamond (n = 2.417).
3. If a substance has a critical angle of 60 degrees, what is its index of refraction?
4. What is the critical angle of air (n = 1.0028). One of the classes did this already.
5. (Review problem.) A 475 nm light ray hits a tank of water (n = 1.33) at an angle of 30 degrees with respect to the normal line. Find the angle of refraction, speed and wavelength inside the water.
6. Prep for the next formal lab. To do this, research the following:
a. focal length. What is the definition?
b. Our next lab will investigate the question: what is the relationship between the location of an object (how close it is to a lens) and whether or not an image forms, and the nature of the image that forms (bigger or smaller image, where it forms, etc.). Decide on a type of protocol to investigate these questions.
1. Review the concept of critical angle and the related formula.
2. Calculate the critical angle of diamond (n = 2.417).
3. If a substance has a critical angle of 60 degrees, what is its index of refraction?
4. What is the critical angle of air (n = 1.0028). One of the classes did this already.
5. (Review problem.) A 475 nm light ray hits a tank of water (n = 1.33) at an angle of 30 degrees with respect to the normal line. Find the angle of refraction, speed and wavelength inside the water.
6. Prep for the next formal lab. To do this, research the following:
a. focal length. What is the definition?
b. Our next lab will investigate the question: what is the relationship between the location of an object (how close it is to a lens) and whether or not an image forms, and the nature of the image that forms (bigger or smaller image, where it forms, etc.). Decide on a type of protocol to investigate these questions.
Tuesday, November 20, 2012
More Snell's Law fun!
(Trig practice)
1. Consider a triangle with sides 20,21, and 29. Find all the angles in the triangle.
2. Choose any other Pythagorean triple and find the angles in the triangle:
(Snell's Law)
3. A 450 nm blue light ray hits a piece of Plexiglas (n = 1.6) at an angle of 55 degrees with respect to a normal line. Find the following:
a. picture that represents what happens
b. angle inside Plexiglas
c. wavelength inside Plexiglas
d. speed of light inside Plexiglas
4. Light hits a piece of unknown material, such that the light refracts from 60 degrees to 35 degrees. If the light enters from air, what is the index of refraction of the material?
5. Review all of the relevant formulas discussed so far to make sure you understand each one. Include the new ones from class today.
Thursday, November 15, 2012
Wednesday, November 14, 2012
Monday, November 12, 2012
Sample Doppler problem
Consider a siren that has a 1200 Hz tone attached to an ambulance traveling at 35 m/s. Find the following frequencies:
a. what you hear when the ambulance approaches you
b. what you hear when the ambulance travels away from
c. what you hear if you were in a car traveling toward the ambulance, you moving at 15 m/s
a. what you hear when the ambulance approaches you
b. what you hear when the ambulance travels away from
c. what you hear if you were in a car traveling toward the ambulance, you moving at 15 m/s
Interesting and cool - not physics related, but math and politics related
http://www-personal.umich.edu/~mejn/election/2012/
Test Friday - practice problems for recent stuff
1. Doppler effect. A police car approaches you. According to the siren's manufacturer, the frequency is 1000 Hz. How would the frequency change if you were located:
a. behind the car as it passed you
b. in front of the car as it approached you
c. in the car
d. running toward the car, if it were at rest
e. running away from the car, if it were at rest
2. What does the red shift of distant galaxies suggest?
3. What do red shift and blue shift mean?
4. Explain the Doppler effect.
5. Consider a 320 Hz note (E, approximately). What is the frequency of:
a. the next E (one octave above)
b. the E one octave below
c. an E that is 3 octaves above
d. an F, one semi-tone above
e. a G, three semi-tones above
Don't forget to review strings, organ pipes and all other wave phenomena.
a. behind the car as it passed you
b. in front of the car as it approached you
c. in the car
d. running toward the car, if it were at rest
e. running away from the car, if it were at rest
2. What does the red shift of distant galaxies suggest?
3. What do red shift and blue shift mean?
4. Explain the Doppler effect.
5. Consider a 320 Hz note (E, approximately). What is the frequency of:
a. the next E (one octave above)
b. the E one octave below
c. an E that is 3 octaves above
d. an F, one semi-tone above
e. a G, three semi-tones above
Don't forget to review strings, organ pipes and all other wave phenomena.


Reflection - light "bouncing" off a reflective surface. This obeys a simple law, the law of reflection!
The incident (incoming) angle equals the reflected angle. Angles are generally measured with respect to a "normal" line (line perpendicular to the surface).
Note that this works for curved mirrors as well, though we must think of a the surface as a series of flat surfaces - in this way, we can see that the light can reflect in a different direction, depending on where it hits the surface of the curved mirror. More to come here.
Refraction is much different. In refraction, light enters a NEW medium. In the new medium, the speed changes. We define the extent to which this new medium changes the speed by a simple ratio, the index of refraction:
n = c/v
In this equation, n is the index of refraction (a number always 1 or greater), c is the speed of light (in a vacuum) and v is the speed of light in the new medium.
The index of refraction for some familiar substances:
vacuum, defined as 1
air, approximately 1
water, 1.33
glass, 1.5
polycarbonate ("high index" lenses), 1.67
diamond, 2.2
The index of refraction is a way of expressing how optically dense a medium is. The actual index of refraction (other than in a vacuum) depends on the incoming wavelength. Different wavelengths have slightly different speeds in (non-vacuum) mediums. For example, red slows down by a certain amount, but violet slows down by a slightly lower amount - meaning that red light goes through a material (glass, for example) a bit faster than violet light. Red light exits first.
In addition, different wavelengths of light are "bent" by slightly different amounts. This is trickier to see. We will explore it soon.
FYI:
http://www.physicsclassroom.com/class/refln/
http://www.physicsclassroom.com/class/refln/
>
http://www.physics.uoguelph.ca/applets/Intro_physics/refraction/LightRefract.html
Refraction, in gross gory detail
 Consider a wave hitting a new medium - one in which is travels more slowly. This would be like light going from air into water. The light has a certain frequency (which is unchangeable, since its set by whatever atomic process causes it to be emitted). The wavelength has a certain amount set by the equation, c = f l, where l is the wavelength (Greek symbol, lambda).
Consider a wave hitting a new medium - one in which is travels more slowly. This would be like light going from air into water. The light has a certain frequency (which is unchangeable, since its set by whatever atomic process causes it to be emitted). The wavelength has a certain amount set by the equation, c = f l, where l is the wavelength (Greek symbol, lambda).
When the wave enters the new medium it is slowed - the speed becomes lower, but the frequency is fixed. Therefore, the wavelength becomes smaller (in a more dense medium).
Note also that the wave becomes "bent." Look at the image above: in order for the wave front to stay together, part of the wave front is slowed before the remaining part of it hits the surface. This necessarily results in a bend.
The general rule - if a wave is going from a lower density medium to one of higher density, the wave is refracted TOWARD the normal (perpendicular to surface) line. See picture above.
Thursday, November 8, 2012
HW and test
Test in 3 classes - next Friday.
HW - each student should attempt to summarize what was seen in the lab. Use the falstad website to help "see" the phenomena, especially the difficult stuff. Write down some bullet-points or comments about each of the parts of the lab.
This semi-formal group lab will be submitted in 2 classes - you'll have some time next class to pull together your data/conclusions/thoughts.
Hooray!
HW - each student should attempt to summarize what was seen in the lab. Use the falstad website to help "see" the phenomena, especially the difficult stuff. Write down some bullet-points or comments about each of the parts of the lab.
This semi-formal group lab will be submitted in 2 classes - you'll have some time next class to pull together your data/conclusions/thoughts.
Hooray!
Tuesday, November 6, 2012
for Thursday
pre-lab HW
You have a temporary definition of the relevant wave terms from today's class. Now look up formal definitions.
physicsclassroom.com may be useful.
Be prepared for some wave fun on Thursday. Check out the falstad website to get a sense of what you should be seeing.
physicsclassroom.com may be useful.
Be prepared for some wave fun on Thursday. Check out the falstad website to get a sense of what you should be seeing.
TEXT OF LAB IS BELOW.
text of the lab
Waves in a Ripple Tank - a
semi-formal group lab
This is a bit of a strange
lab. First, it is a group lab - to be
submitted by the group as one document.
You will witness waves in a different fashion than we have in the last several
classes: waves in water. This is useful, as light (our next topic)
behaves in a wave-like fashion under several circumstances.
For this lab, I would like
you to begin by writing your own personal definitions of these words:
Reflection, refraction, diffraction,
interference
This will serve as a
hypothesis. How do you expect to see
these phenomena represented in water?
This is a largely visual, non-quantitative lab. Enjoy!
For your "data",
draw everything you see and make relevant comments. Each lab partner should do this in his or her
lab notebook.
1. Propagation of waves
Dip your finger in the water
repeatedly, with constant frequency.
Comment. We will call these
"circular waves" in this lab.
Do the same with a ruler,
commenting on what is seen. We will call
these "straight waves" in this lab.
2. Reflection of waves
Send a wave (or waves) into a
barrier. Try this directly (no angle) at
first, and then at some angle. Discuss.
3. Refraction of waves
This can be tricky to see,
but there is something to be observed.
Set up an area with deep water and shallow water (using a piece of
Plexiglas) to see what happens when water passes from one medium (deep) to
another (shallow), or vice versa. Try
this directly and also at an angle (as above).
4. Diffraction of waves
Send straight waves to a
barrier as shown.
Now send them through a small
opening, changing the size of the opening and noting the effects. Comment on all scenarios.
5. Interference of waves
This can also be tough to
see. Instead of creating one set of
circular waves, create 2 sets (with 2 fingers) at the same frequency. Watch what happens when they
"interact" with each other.
Comment and draw if at all possible
Some of these things can be
tough to see. You may want to play with the
applet below to see what would be seen under ideal circumstances for some of
these cases.
http://falstad.com/ripple/
In your group's conclusion,
comment on what you saw, especially as it relates to what you thought you'd
see. Give updated definitions of the
words initially mentioned in the lab introduction.
pre-lab HW
You have a temporary definition of the relevant wave terms from today's class. Now look up formal definitions.
physicsclassroom.com may be useful.
Be prepared for some wave fun on Thursday. Check out the falstad website to get a sense of what you should be seeing.
physicsclassroom.com may be useful.
Be prepared for some wave fun on Thursday. Check out the falstad website to get a sense of what you should be seeing.
Thursday, November 1, 2012
FYI - just for fun
http://www.youtube.com/watch?v=AcS3NOQnsQM&feature=related
The classic "Elements song".
http://www.youtube.com/watch?v=U0kXkWXSXRA&feature=related
A new "classic"? Or not.
The classic "Elements song".
http://www.youtube.com/watch?v=U0kXkWXSXRA&feature=related
A new "classic"? Or not.
Friday, October 26, 2012
post-quiz HW
Read about the Doppler effect. If possible, find an equation that describes it and identify the variables involved.
Monday, October 22, 2012
Practice for Friday's quiz
1. Differentiate between mechanical and electromagnetic waves. Give examples.
2. Draw a wave and identify the primary parts.
3. Find the speed of a 500 Hz wave with a wavelength of 0.4 m.
3. What is the frequency of a wave that travels at 24 m/s, if 3 wavelengths of the wave fit in a 12-m space. (Hint: find the wavelength first.)
4. Approximately how much greater is the speed of light than the speed of sound?
5. Draw the first 3 harmonics for a wave on a string. If the length of the string is 1-m, find the wavelengths of these harmonics.
6. Show how to compute the wavelength of WTMD's signal (89.7 MHz). Note that MHz means 'million Hz."
7. Explain the Chladni plate seen in class.
8. A C-note vibrates at 262 Hz (approximately). Find the frequencies of the next 2 C's (1 and 2 octaves above this one).
*9. Given a 440 Hz concert A, find the following frequencies: one octave below, the note A# (one semi-tone above), the note B (2 semi-tones above).
*10. Explain the Ruben's tube from class.
*11. Consider an organ pipe 0.5-m long. If the speed of sound is 340 m/s, find (and draw) the first 3 harmonics (wavelengths and frequencies).
Tuesday, October 16, 2012
Recent notes on waves
There are 2 primary categories of waves:
Mechanical – these require a medium (e.g., sound, guitar
strings, water, etc.)
Electromagnetic – these do NOT require a medium and, in
fact, travel fastest where is there is nothing in the way (a vacuum). All e/m waves travel at the same speed in a
vacuum (c, the speed of light)
General breakdown of e/m waves from low frequency (and long
wavelength) to high frequency (and short wavelength):
Radio
Microwave
IR (infrared)
Visible (ROYGBV)
UV (ultraviolet)
X-rays
Gamma rays
In detail, particularly the last image:
Waves have several characteristics associated with them,
most notably: wavelength, frequency,
speed. These variables are related by
the expression:
v = f l
speed = frequency x wavelength
For e/m waves, the speed is the speed of light, so the
expression becomes:
c = f l
Note that for a given medium (constant speed), as the
frequency increases, the wavelength decreases.
Note the units:
Frequency is in hertz (Hz), also known as a cycle per
second.
Wavelength is in meters or some unit of length.
Speed is typically in meters/second (m/s).
Sound waves
In music, the concept of “octave” is defined as doubling the
frequency. For example, a concert A is
defined as 440 Hz. The next A on the
piano would have a frequency of 880 Hz.
The A after that? 1760 Hz. The A below concert A? 220 Hz.
Finding the other notes that exist is trickier and we’ll get to that
later.
Waves can “interfere” with each other – run into each
other. This is true for both mechanical
and e/m waves, but it is easiest to visualize with mechanical waves. When this happens, they instantaneously
“add”, producing a new wave. This new
wave may be bigger, smaller or simply the mathematical sum of the 2 (or more)
waves. For example, 2 identical sine
waves add to produce a new sine wave that is twice as tall as one alone. Most cases are more complicated.
In music, waves can add nicely to produce chords, as long as
the frequencies are in particular ratios.
For example, a major chord is produced when a note is played
simultaneously with 2 other notes of ratios 5/4 and 3/2. (In a C chord, that requires the C, E and G
to be played simultaneously.) Of course,
there are many types of chords (major, minor, 7ths, 6ths,…..) but all have
similar rules. In general, musicians don’t
remember the ratios, but remember that a major chord is made from the 1 (DO),
the 3 (MI) and the 5 (SO). It gets
complicated pretty quickly.
We looked at specific cases of waves interfering with each
other – the case of “standing waves” or “harmonics.” Here we see that certain frequencies produce
larger amplitudes than other frequencies.
There is a lowest possible frequency (the resonant frequency) that gives
a “half wave” or “single hump”. Every
other harmonic has a frequency that is an integer multiple of the resonant
frequency. So, if the lowest frequency
is 25 Hz, the next harmonic will be found at 50 Hz – note that that is 1 octave
higher than 25 Hz. Guitar players find
this by hitting the 12th fret on the neck of the guitar. The next harmonics in this series are at 75
Hz, 100 Hz and so on.
Subscribe to:
Posts (Atom)
.JPG)


.JPG)
.JPG)
.JPG)
.JPG)
.JPG)